Machine Learning - Bayesian Linear Regression을 이용한 보험 비용 예측하기 Part2

데이터 출처 : www.kaggle.com/teertha/ushealthinsurancedataset

US Health Insurance Dataset

 

ipynb file : github.com/sangHa0411/DataScience/blob/main/Insurance_Charges.ipynb

sangHa0411/DataScience

 

이전 포스팅에서 데이터 분석 및 특성 선택을 하였습니다.

 

이제 이를 통해서 Bayesian Linear Regression을 해보도록 하겠습니다.

 

Bayesian Linear Regression에 대해서는 아래의 참고 자료에 잘 설명이 되어있습니다.

참고자료1 : towardsdatascience.com/introduction-to-bayesian-linear-regression-e66e60791ea7

Introduction to Bayesian Linear Regression

 

아래는 위 참고자료에서 특정 부분을 발췌한 내요입니다.

Bayesian Linear Regression을 정리해보자면 Linear Regression을 할 떄 특정 수치로 회귀를 하는 것이 아니라 해당 값의 확률 분포로 나타내는 것이 목표입니다.

위 선형 회귀의 값인 y값을 정규 분포로써 나타낸 것을 의미합니다.

 

목표는 앞서 말씀드린 것과 같이 특정 값을 얻고자 하는 것이 아니라 특정 값의 분포를 얻고자 하는 것입니다.

이는 사전에 분포가 어떻게 될 것이다 라고 예측하는 사전 확률 분포와 주어진 데이터를 이용해서 최종적인 사후 확률 분포를 구하는 것입니다.

 

실제 위 원리를 기반으로해서 사후 확률 분포를 구하는 것은 매우 복잡한 과정을 요구합니다. 하지만 파이썬에서는 pymc3 라이브러리가 있는데 이를 이용해서 간편하게 이용 및 구현할 수 있습니다.

 

먼저 Part1에서의 결과를 간략하게 정리하겠습니다.

 

먼저 청구 비용과 상관 없다고 판단된 children 과 region 특성은 선형 회귀에서 사용하지 않도록 특성에서 제외시킵니다.

그리고 데이터와 레이블을 구분합니다.

그리고 훈련 데이터와 테스트 데이터 비율을 80% 과 20%로 분할합니다.

 

그리고 이는 연속적인 속성과 이산적인 속성 데이터가 섞여있는데 이산적인 속성은 정수로 인코딩하겠습니다.

 

그리고 훈련 데이터를 이용해서 ColumnTransformer를 학습시킵니다.

 

그리고 이를 이용해서 훈련 데이터 및 테스트 데이터를 변환시킵니다.

 

그리고 레이블에 해당되는 데이터 값을 1000으로 나누어주어서 전처리를 해줍니다.

위 변환된 데이터를 확인해본 결과 이산적인 데이터가 인코딩된 결과인 2개만 존재하는 것을 확인할 수 있습니다.

 

여기에 연속적인 속성값에 속성을 추가시켜줄려고 합니다.

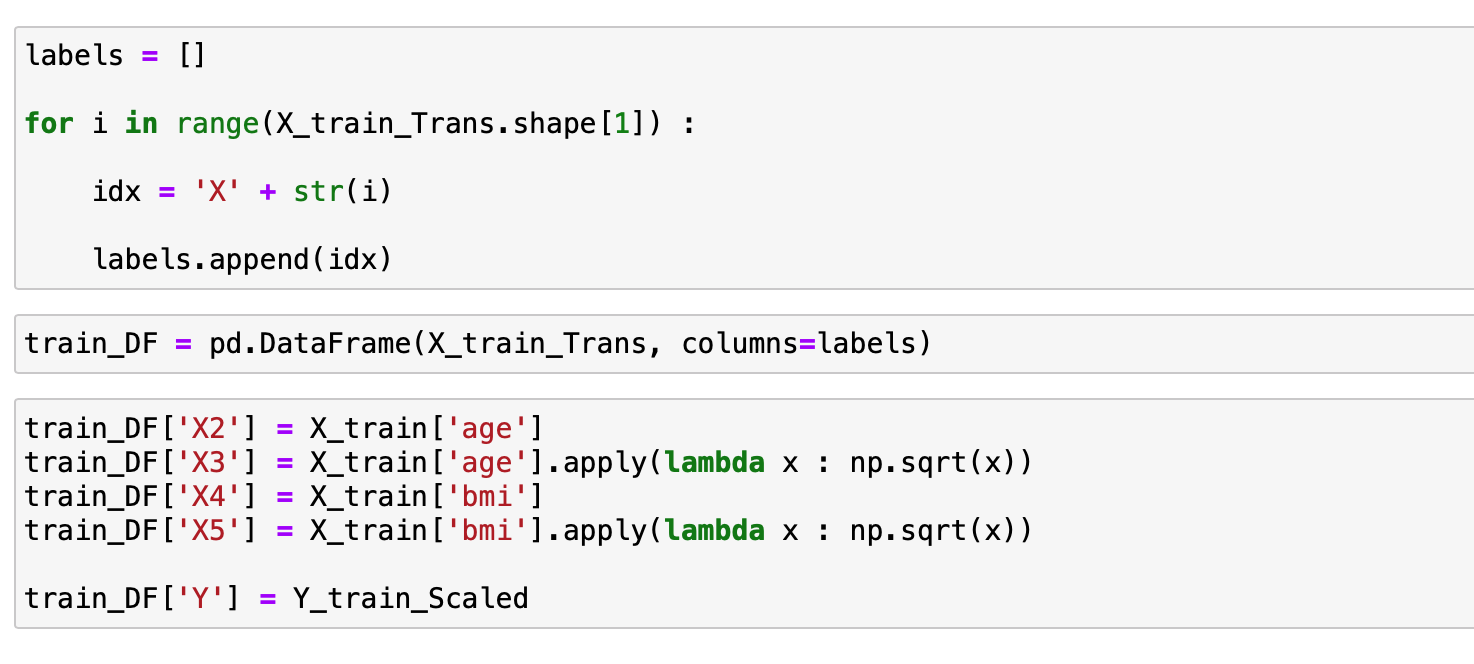
연속적인 속성에다가 루트를 씌운 값을 추가로 해서 연속적인 속성을 총 4개 추가해줍니다.

 

이를 통해서 만든 Data Frame은 아래와 같습니다.

 

속성은 X0 ~ X5 까지 총 6개의 속성이 있고 이를 통해서 Y값을 예측하는 것이 목표입니다.

 

먼저 Bayesian Linear Regression을 하기위한 라이브러리를 가져옵니다.

 

그리고 Linear Regression을 하기위한 형식을 정해줍니다.

이 형식의 의미는 X0 ~ X5를 이용해서 Y를 회귀하곘다는 것을 의미합니다.

 

이제 최종적으로 Bayesian Linear Regression을 pymc3을 이용해서 구현해보겠습니다.

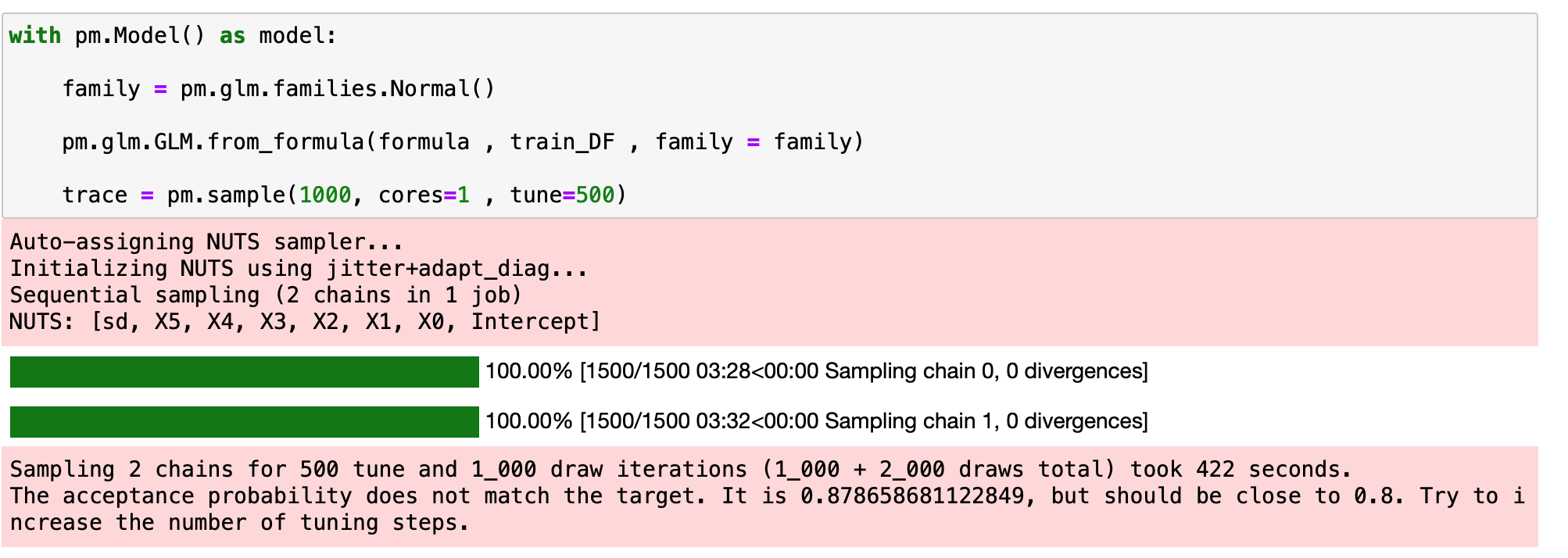
먼저 사전 분포를 정규분포라고 가정을 합니다,

그리고 이 가정과 위에서 정한 formula 그리고 Pandas DataFrame의 데이터를 인자로 입력합니다.

여기서 사후 확률 분포를 바로 얻을 수 없어서 여러 샘플을 얻어서 사후 확률 분포를 구하는데  이를 pm.sample 함수를 이용해서 실행합니다.

이에 대해서는 위 참고자료를 읽어보시면 확인하실 수 있습니다.

아래는 위 참고자료에서 발췌한 내용입니다.

 

이제 최종적인 학습 결과를 확인해보겠습니다.

각 변수 X0 , X1 , X2 등의 변수의 평균 값 , 표준편차 등의 값이 나와있는 것을 확인할 수 있습니다.

 

이를 그래프로 표현해보겠습니다.

 

사후 확률 분포에 대해서 파악하기 쉽게 그래프를 그려주는 라이브러리 함수도 존재합니다.

 

저는 이 각 변수의 사후 확률 분포의 평균 값을 이용해서 선형 회귀를 해보도록 하겠습니다.

 

그를 위해서 test 데이터를 변환해보겠습니다.

 

각 변수의 사후 확률 분포의 평균 값을 최종 확인합니다.

 

그리고 이 평균 값과 테스트 데이터 값을 이용해서 청구 비용의 값을 구하는 함수를 정의합니다.

 

input._vec에 1을 추가하는 이유는 이 값과 Intercept과 대응시키기 위해서입니다.

따라서 저희는 Intercept , X0 ~ X5 총 7개의 평균 값과 테스트 데이터에 1을 추가한 input Vec과 연결해서 청구 비용을 예측합니다.

 

정리하면 -21.635 -0.204(X0) + 23.717(X1) + 0.607(X2) -4.238(X3) - 0.411(X4) + 8.154(X5) = Y 이 선형 회귀의 식이 되는 것입니다.

 

회귀 문제이므로 rmse 로써 모델의 Error 값을 구합니다.

 

 

예측 값과 실제 값을 그래프로 그려서 비교해보겠습니다.

 

추가적으로 테스트 데이터에서 인덱스 값을 무작위로 선정해서 해당 출력 값의 확률 분포를 구해보겠습니다.

여기서는 앞서 회귀에서 사용하지 않았던 sd 값을 이용해야 합니다.

 

회귀로 예측한 값을 평균 값으로 선정하고 표준편차를 앞서 확인한 6.084로 지정한 다음에 정규 분포를 구합니다.

 

이제 이 정규분포와 실제 청구 비용의 값을 비교해보겠습니다.

 

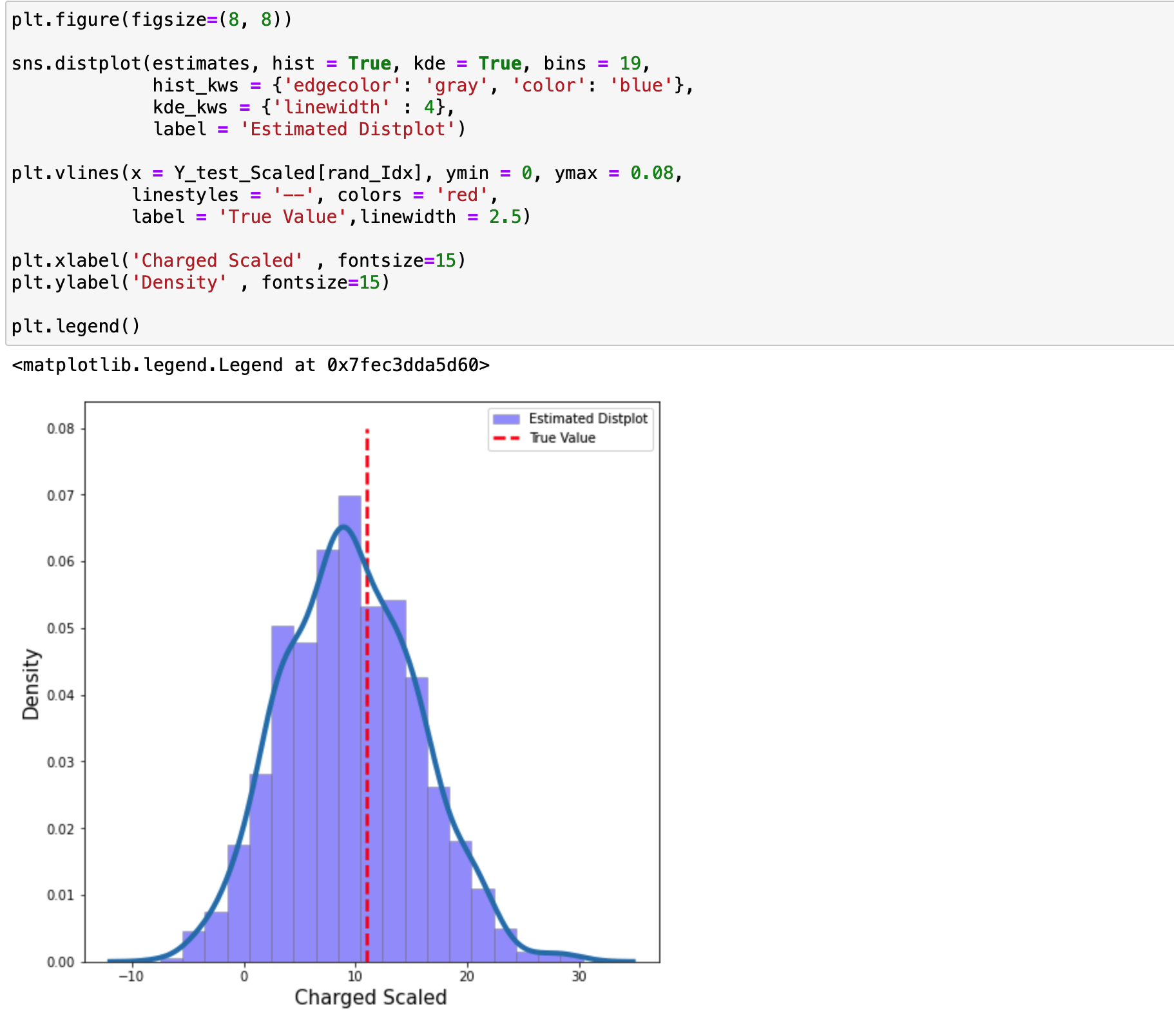
이제 최종적으로 Bayesian Linear Regression의 장점에 대해서 정리해보겠습니다.

 

먼저 저희는 청구 비용이 정규분포를 이룰 것이다 라고 짐작을 해서 정규 분포로 사전 분포를 결정하였지만 만일 우리가 도메인 지식이 있는 분야에 대해서 모델을 설계했다면 이 도메인 지식을 이용해서 사전 확률 분포를 지정해줄 수가 있습니다.

그리고 특정 값을 구하는 것이 아니라 해당 값의 확률 분포를 구하는 것으로써 데이터가 불확실성에 대해서 어느정도 표현이 가능해집니다.

데이터가 많으면 많을 수록 더 정교해지겠지만 데이터가 적을 수록 사후 확률 분포가 더 옆으로 퍼짐으로써 불확실성이 늘어나게 됩니다. 이를 저희가 직접 관찰하고 파악할 수 있게 됩니다.